odd function integral|5.5: Indefinite Integrals and the Substitution Rule : Manila A definite integral is either a number (when the limits of integration are constants) or a single function (when one or both of the limits of integration are variables). An indefinite integral represents a family of functions, all .
With a stay at Solitaire Bangkok Sukhumvit 11, you'll be centrally located in Bangkok, within a 5-minute drive of Terminal 21 Shopping Mall and Siam Paragon Mall. This 4.5-star hotel is 2.1 mi (3.5 km) from Pratunam Market and 4.8 mi (7.8 km) from Khaosan Road. Relax and unwind with massages and body treatments.
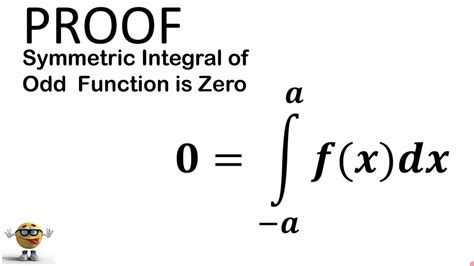
odd function integral,The graphs of even functions are symmetric about the [Math Processing Error] y -axis. An odd function is one in which [Math Processing Error] f ( − x) = − f ( x) for all [Math Processing Error] x in the domain, and the .
5.5: Indefinite Integrals and the Substitution RuleAbr 17, 2018 — Sometimes we can simplify a definite integral if we recognize that the function we’re integrating is an even function or an odd function. If the function is neither even nor odd, then we proceed .
Learn how to find integrals of even and odd functions on symmetric intervals using properties and special methods. See examples, solutions, and tips for evaluating .
Okt 3, 2021 — Let $f$ be an odd function with a primitive on the open interval $\openint {-a} a$, where $a > 0$. Then the improper integral of $f$ on $\openint {-a} a$ is: $\ds .
odd function integralSet 2, 2012 — If the range of the definite integral is -a to a, and if the function is odd, then the value of the integral is 0. To determine if the function is odd, plug -x in for x, and then simplify. If.A definite integral is either a number (when the limits of integration are constants) or a single function (when one or both of the limits of integration are variables). An indefinite integral represents a family of functions, all .odd function integral 5.5: Indefinite Integrals and the Substitution RuleEne 21, 2022 — Example 1.2.11 Odd functions. Three examples of odd functions are \(f(x)=\sin x\text{,}\) \(f(x)=\tan x\) and \(f(x)=x^3\text{.}\) In fact, if \(f(x)\) is any odd power .Hun 5, 2021 — More integration tutorials:Integration with substitution: https://youtu.be/rv6LpW-YDyoPartial Integration: https://youtu.be/9517JtKv630Integration with t-for.
Integrals of odd functions, when the limits of integration are similarly [− a, a], [− a, a], evaluate to zero because the areas above and below the x-axis are equal. Rule: .Integration of Even and Odd Functions. Letf be continuous on the interval [-a,a] 1. If f is an even function, then. ∫-aaf(x)dx=2∫0af(x)dx. 2. If f is an odd function, then. ∫-aaf(x)dx=0. EXAMPLE - Integrating Even and Odd .
Example 1: Identify whether the function f(x) = sinx.cosx is an even or odd function.Verify using the even and odd functions definition. Solution: Given function f(x) = sinx.cosx.We need to check if f(x) is even or odd. .
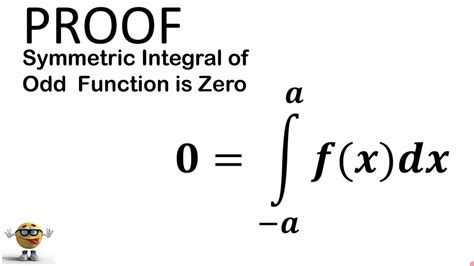
May 3, 2017 — So, simple question; why does WolframAlpha fail to evaluate infinite bounded definite integrals of odd functions, stating that the solution "does not converge"? Is it not exactly accurate to say that the answer is zero? Edit: Rather, I should say that the integral over symmetric bounds, in general, of an odd function is zero. Why when we use .
The product of any two odd functions is an even function. The quotient of any 2 odd functions is an even function. Composition: The composition of any 2 odd functions is odd. The derivative of any given odd function .Nob 16, 2022 — As noted above we simply can’t integrate functions that aren’t continuous in the interval of integration. Also, even if the function was continuous at \(x = 1\) we would still have the problem that the function is actually two different equations depending where we are in the interval of integration. . Even and Odd Functions. This is the .Peb 6, 2020 — Improper Integral - Odd Function and Symmetric range but Diverge. 3. Improper integral with parameter. 2. Finding improper integral (depending on a parameter) 0. Example of divergent improper integral. 0. Indefinite integral of an odd function. Hot Network Questions
Nob 27, 2015 — $\begingroup$ Since $\sin(x)$ is an odd function, with period $2\pi$, it's integral over any interval of length $2\pi$ is zero. As for the other two terms, can you show what you've tried so far? $\endgroup$ –
Peb 25, 2022 — Even and Odd Functions. During the course of our study of integrals of functions of one variable, we found that the evaluation of certain integrals could be substantially simplified by exploiting symmetry properties of the integrand. Concretely, in Section 1.2.1 of the CLP-2 text, we gave the
They are special types of functions. Even Functions. A function is "even" when: f(x) = f(−x) for all x In other words there is symmetry about the y-axis (like a reflection):. This is the curve f(x) = x 2 +1. They are called "even" functions because the functions x 2, x 4, x 6, x 8, etc behave like that, but there are other functions that behave like that too, such as .Several common types of functions have graphs that are symetric with respect to the y-axis or the origin, as shown in the next Figures. If the graph of y = f(x) is symmetric with respect to the y-axis, then we call f an even function. Similarly, if the graph of y = f(x) is symmetric with the respect to the origin, then we call f an odd function.Hun 5, 2021 — More integration tutorials:Integration with substitution: https://youtu.be/rv6LpW-YDyoPartial Integration: https://youtu.be/9517JtKv630Integration with t-for.
$\begingroup$ Is it given that the function is odd and thus you prove that the integral is zero, or is it given that the integral is zero and thus the function is odd? That's not clear. It seems like the second, but then the trouble starts with your second line" because the function.." $\endgroup$ –
Ago 13, 2020 — 0:00 Integrals of Even and Odd Functions and the Function Average.0:25 Introduction to Even Functions.3:56 Introduction to Even Functions.6:31 Trig Functions.
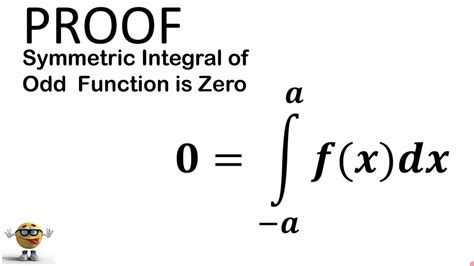
The odd functions are functions that return their negative inverse when x is replaced with –x. This means that f(x) is an odd function when f(-x) = -f(x). Learn how to plot an odd function graph and also check out the solved examples, practice questions. Grade. KG. 1st. 2nd. 3rd. 4th. 5th. 6th. 7th. 8th. Algebra 1. Algebra 2. Geometry. Pre .5.4.4 Apply the integrals of odd and even functions. In this section, we use some basic integration formulas studied previously to solve some key applied problems. It is important to note that these formulas are presented in terms of indefinite integrals. Although definite and indefinite integrals are closely related, there are some key .Peb 8, 2022 — The integration was not difficult, and one could easily evaluate the indefinite integral by letting \(u=\sin x\) or by letting \(u = \cos x\). This integral is easy since the power of both sine and cosine is 1. We generalize this integral and consider integrals of the form \(\int \sin^mx\cos^nx\ dx\), where \(m,n\) are nonnegative integers.
Mar 21, 2023 — Prove that a symmetric integral of an odd function is zero. This is true if the limits go from -a to a.I've got tons of integrals in my integrals playlist! C.The "what is" part has already be answered by Alex White. The "how does it help in integration" part is easy: If your integration interval is symmetric around $0$ (which especially includes integration over all of $\mathbb R$), then the integral over any integrable odd function is zero, no exception. Therefore as soon as you've found that .
odd function integral|5.5: Indefinite Integrals and the Substitution Rule
PH0 · Integration trick
PH1 · Integration of Even and Odd Functions
PH2 · Integrating Even and Odd Functions
PH3 · Integrals of even/odd functions — Photomath
PH4 · Definite integrals of even and odd functions
PH5 · Definite integral of an odd function (KristaKingMath)
PH6 · Definite integral of an odd function (KristaKingMath
PH7 · Definite Integral of Odd Function
PH8 · 5.5: Indefinite Integrals and the Substitution Rule
PH9 · 5.4 Integration Formulas and the Net Change Theorem
PH10 · 1.2: Basic properties of the definite integral